Recommendation_System

Project overview

• Developed a movie recommendation system using matrix factorization techniques.
• Compared two methods: ALS implemented from scratch versus SVD using the Surprise library.
• The scratch-built model slightly outperformed the library-based model, but with higher complexity and performance.

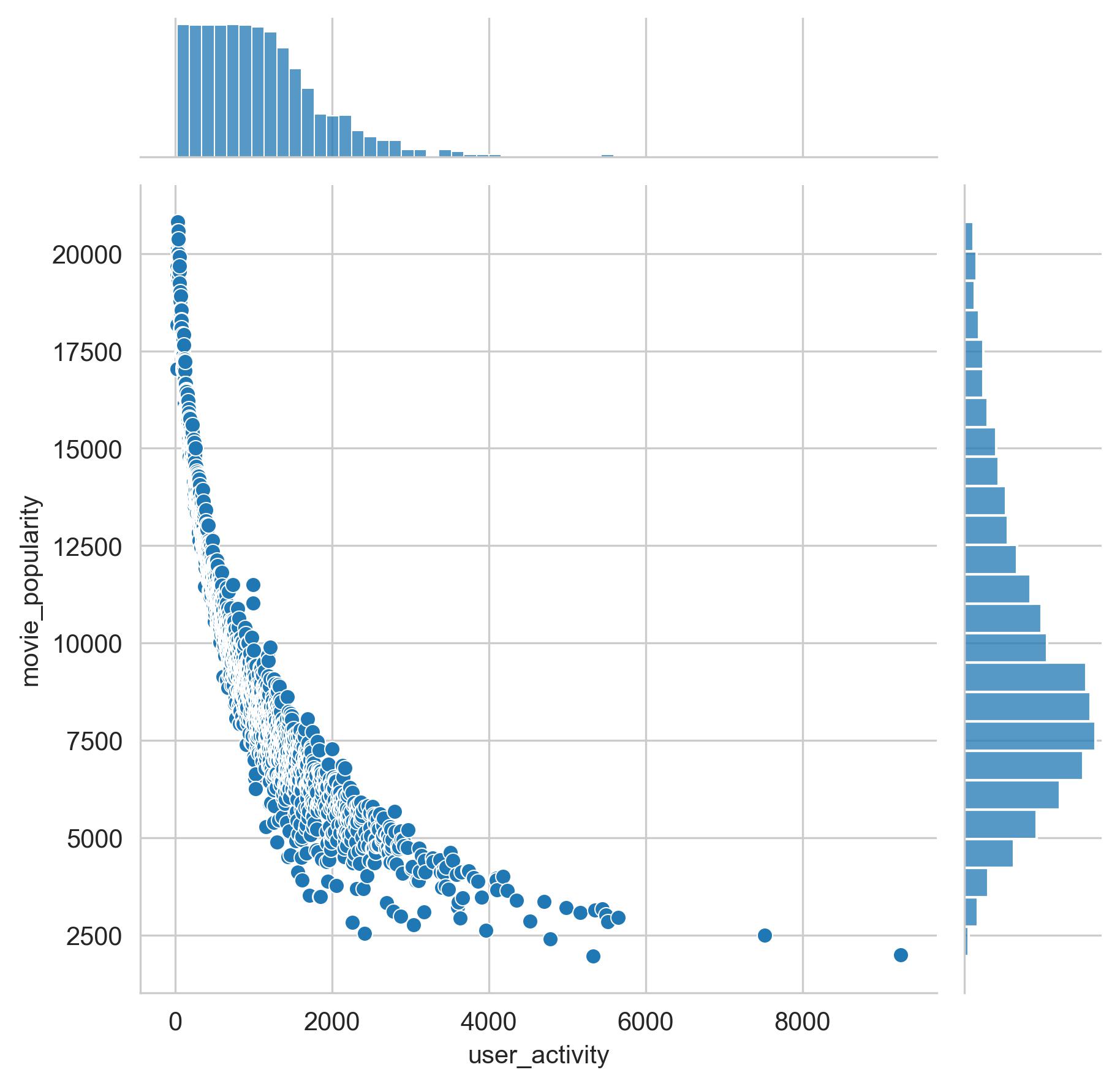
EDA

• Conducted EDA to gain insights into the dataset and its characteristics.
• Key finding: Users who review more movies tend to review less popular titles. See the full code HERE

Data preprocessing

• Reduced the dataset to use the 15,000 most frequent users and 3,000 movies
• Created 3 dictionaries user2movie, movie2user and usermovie2rating for matrix factorization.
• Created user2movierating and movie2userrating dictionaries, which contain the user-movie rating information. See the full code HERE

Model 1: Matrix factorization from scratch

• Implemented a matrix factorization model, where the user factors (W) and item factors (U) are learned to predict the user-item ratings.
• The model includes user biases (b) and item biases (c), which are learned along with the latent factors.
• The update functions alternately optimize the user factors/biases and item factors/biases, using regularized least squares to learn the parameters that minimize the mean squared error between predicted and actual ratings.
• The final results are Train MSE: 0.5125, Test MSE: 0.5126 See the full code HERE

Model 2: Matrix factorization using surprise library

• Implemented a recommendation system using the Surprise library using a SVD (Singular Value Decomposition) model
• Performed K-Fold Cross-Validation with Early Stopping to evaluate the model’s performance, calculating the Mean Squared Error (MSE) on both the training and testing sets for each fold.
• The final results are Train MSE: 0.6308, Test MSE: 0.6377 See the full code HERE

Conclusions

• Model 1 exhibited slightly better performance than Model 2 (0.5126 vs. 0.6377).
• Model 2 was faster overall, though its runtime increased due to Cross-Validation, unlike Model 1, which did not have parameter tuning.
• Model 1 was more complex to code but conceptually simpler, adhering to the formula for regularized least squares.
• Model 1 could benefit from further vectorization to improve its runtime performance but it would make it more complex as it will not follow the regularized least squares formula as much.